La condicional Sí entonces

La Lógica proposicional nos ofrece otro método maravilloso para desarrollar nuestros razonamientos, a partir de los cuales podemos mejorar nuestra argumentación y estilo literario, nos referimos a la condicional Sí-entonces (p → q). La frase citada de Mario Vargas Llosa, Cuanto más inteligente sea nuestro ordenador, más tontos seremos, es una proposición condicional. Esta puede ser expresada de manera más formal, como:

Si los ordenadores son más inteligentes, entonces los seres humanos serán más tontos.

Desde luego, se trata de una falacia lógica, pero que algunos tragan sin masticar.

La condicional Si p, entonces q (p → q), tiene muchos usos y sentidos en la vida cotidiana, pues se puede utilizar para indicar una relación lógica, en la que el consecuente (q) se deduce del antecedente (p). También se puede utilizar para indicar una relación de causa-efecto o como función matemática y se puede aplicar para comunicar una decisión, así como para deducir el consecuente (q) del antecedente (p). Igualmente, se puede usar hasta en forma humorística.

Sí tú eres genio, entonces yo soy Superman, sería un ejemplo del sentido humorístico de la condicional.

La condicional es una proposición que sólo es falsa cuando, siendo el antecedente verdadero, el consecuente es falso, y verdadera en los demás casos. Llamamos ‘antecedente’ de la condicional a la proposición que se halla a su izquierda, y ‘consecuente’ a la que está a su derecha, es decir, el primer elemento es la hipótesis, y el segundo la tesis o conclusión. La siguiente tabla de verdad, revela los valores que asume la condiciona en función del valor de verdad del antecedente y el consecuente:

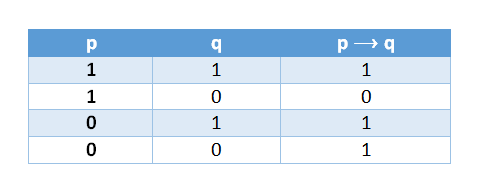
Variantes de la condicional 

La condicional tiene diversas variaciones que son muy útiles no solo para el proceso de razonamiento y desarrollo de textos argumentativos, sino también para matizar literariamente un trabajo de composición. De hecho el solo distinguir los componentes de la condicional, en la cual el antecedente es la hipótesis y el consecuente la tesis, ya deviene en una aclaración, muy útiles a la hora de hacer un trabajo de tesis, pues a los que se inician en el trabajo de investigación muchas veces se les dificultad formular hipótesis.

Las variaciones de la condicional (p→q) son: la recíproca (q→p), la inversa (¬p→¬q) y la contrarecíproca (¬q→¬p). Utilicemos la condicional anterior para ver sus diversas variaciones:

p→q: Si los ordenadores son inteligentes, entonces los seres humanos son tontos.
q→p Si los seres humanos son tontos, las computadoras son inteligentes.
¬p→¬q Si los ordenadores no son inteligentes, entonces los seres humanos no son tontos.
¬q→¬p Si los seres humanos no son tontos, entonces las computadoras no son inteligentes.

La tabla de verdad de la condicional y sus variaciones se ejemplifican en el siguiente cuadro, donde el 1 corresponde a valores de verdad y el 0 a valores de falsedad.

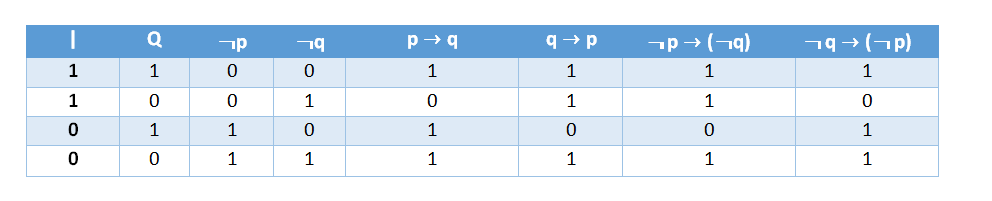Una proposición bicondicional sólo es verdadera si las dos proposiciones tienen el mismo valor de verdad, es decir, son ambas verdaderas o falsas a la vez. Así, por ejemplo:

La bicondicional (↔) es otro de los conectivos importantes de la Lógica, y puede ser usada en la redacción de nuestros textos para darle énfasis a una afirmación.La bicondicional

Si un polígono tiene tres lados, entonces es un triángulo.
Si un polígono es un triángulo, entonces tiene tres lados.
Un polígono es un triángulo, sí y sólo sí tiene tres lados.

Los valores de verdad de la bicondicional se representan en el siguiente cuadro:

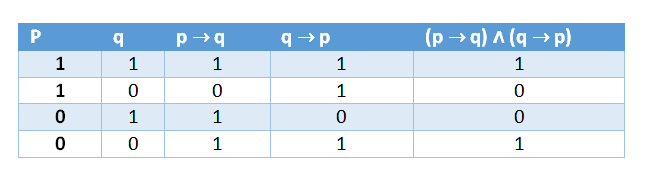Literariamente, la bicondicional puede utilizarse, para dar énfasis a una argumentación. El mejoramiento de la formación matemática y lingüística puede mejorar en forma sustancial, sí y sólo sí, ambas disciplina se estudian en forma simultánea, como una especialidad, puede ser un ejemplo de lo dicho.

¿Es posible establecer un criterio de verdad en base a estos operadores lógicos, en especial sobre temas sociales, económicos y políticos?

Desde luego resulta difícil y complicado traducir muchas expresiones del lenguaje común al lenguaje de la lógica, pues entran en juego procesos más complejos de razonamientos, y desde luego, valores (diversidad de criterios éticos o normativos). Esto hace imposible el sueño de Leibniz de convertir el pensamiento humano en procesos de razonamientos cuyos criterios de verdad puedan ser determinados por una máquina o un sistema de lógico determinado o deductivo. Pero tener de referencia los fundamentos de la Lógica de seguro ayudará a tomar mejores decisiones y establecer criterios de verdad.

La Lógica proposicional es una disciplina que puede ser muy útil para el proceso de redacción y composición de textos argumentativos. Su conocimiento es una herramienta de gran importancia para el conocimiento humano. Aquí hemos apenas hemos esbozado las principales proposiciones y sus conectivos, para destacar como su reutilización puede ser de gran utilidad para la nueva disciplina por la que propugnamos, nos referimos a la Lógica matemática de la redacción.

(Lógica matemática de la redacción y otros libros del autor, se pueden encontrar en Amazon)